Le sudoku sur le site www.sudokunew.com
- Raoul Salzberg
- 8 mai 2024
- 16 min de lecture

Sommaire
Introduction
Description de l’application de sudoku sur le site www.sudokunew.com
Principe du jeu de sudoku
L’interface d’accueil du site
Les 3 types de grilles (implantées dans le programme, créées à partir de revues, générées)
Les 3 types de résolution (manuelle, calcul avec des méthodes, calcul complet)
Le développement d’applications
Historique succincte de la programmation informatique
L’avènement d’internet et les nouvelles méthodes de programmation
Une nouvelle manière de développer des applications sur internet
Le cahier des charges d’un logiciel de bridge
Les données
L’interface d’accueil
Les enchères
La feuille de convention
Les ouvertures et les réponses du standard français
Les interventions derrière l’ouverture
Les enchères compétitives
Les barrages
Le Blackwood 5 clés
Le jeu de la carte
Le déclarant
La défense
Conclusion
Introduction
Le marché des applications sur internet est porteur, dont un segment est occupé par l’intelligence Artificielle (réseaux neuronaux avec convolution, ChatGPT).
Le langage de base internet (HTML, CSS, javascript) est utilisé essentiellement pour les jeux, le reste étant monopolisé par les frameworks, qui sont des surcouches logicielles plutôt dédiées à la gestion (banques, assurances, comptabilité, logistique, process industriels).
Le logiciel de sudoku sur le site internet www.sudokunew.com, a été réalisé avec les langages de base internet. Il utilise pour cela les standards élaborés par le W3C (World Wide Web), porté par des millions de développeurs dans le monde, en continuelle évolution. Il s’est appuyé sur les sites d’aide au développement en ligne comme W3Schools.
Ce site de sudoku est en open source, et peut constituer, en tant qu’application réussie, une base de développement pour d’autres applications.
Son auteur propose de démontrer la portabilité de ce programme, en l’utilisant comme modèle pour développer, dans les 6 mois qui viennent, un logiciel de bridge sur internet, compétitif avec les applications de bridge existantes sur internet.
Description de l’application de sudoku sur le site www.sudokunew.com
Principe du jeu de sudoku
Le jeu de sudoku est un jeu solitaire sur un diagramme carré de 81 cases. La règle du jeu consiste à disposer sur ce diagramme des chiffres de 1 à 9, tels que aucune case affectée avec un chiffre ne puisse voir, dans aucune des 3 zones de 9 cases (ligne, colonne ou bloc) où se trouve cette case, une autre case avec ce chiffre.
A partir d’une grille de départ contenant au minimum 17 cases affectées par un chiffre, respectant la contrainte ci-dessus, il s’agit de trouver une grille finale où toutes les 81 cases sont affectées, respectant cette contrainte.
L’interface d’accueil du site
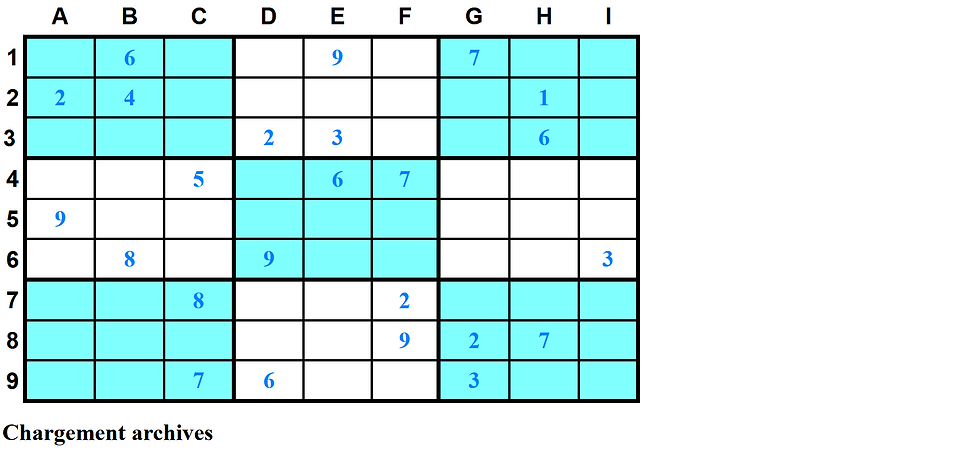
Au chargement du programme, c’est cette interface qui apparaît.
Avec une grille, choisie aléatoirement parmi les grilles faciles, nommée ici « Amandier », dans son archive nommée « 50 grilles faciles générées ». Cette grille a été générée avec la fonction de génération de grilles du programme. Elle est non effaçable, et fait partie de 4 archives de base, implantées en dur dans le programme.
Les 10 icônes en haut de cet écran, ont les fonctions suivantes, dans l’ordre :
Impression de l’écran d’accueil dédié à la résolution manuelle de la grille
Transfert vers l’écran de calcul de la grille par ordinateur
Basculement faisant apparaître les chiffres-candidats des cases
Choix aléatoire d’une nouvelle grille du programme
Annulation de la dernière opération manuelle
Affichage de l’Aide imprimable, sur 150 pages, dans un écran séparé
Affichage des méthodes de résolution, dans une liste sous la grille
Création d’une grille, avec grille initiale vierge, pour en faire une saisie
Enregistrement grille dans une archive personnelle (hors des 4 archives de base)
Suppression de la grille personnelle
Ces icônes sont suivies d’un menu déroulant permettant de sélectionner le niveau de difficulté de la grille choisie aléatoirement parmi les grilles du programme, lorsqu’ensuite on clique sur l’icône de choix de cette grille.
A droite du menu déroulant se trouve une case à cocher, qui permet de fournir une aide à l’utilisateur qui essaie de résoudre manuellement cette grille. Cela se manifeste par l’apparition du symbole ! à la fin du message sous la grille, indiquant que l’opération manuelle en cours est correcte.
Sous la grille se trouve la zone des messages indiquant quelle est l’opération en cours (chargement de grille, saisie manuelle d’un chiffre dans une case, effacement de la grille, annulation de la dernière opération manuelle, etc.).
Sous la zone des messages se trouve la zone des listes : historique des étapes de calcul (manuelles ou par ordinateur), liste des méthodes de résolution pour impossibilité, liste des méthodes de résolution pour défaut d’unicité, liste des variantes des méthodes (chaque méthode pouvant donner plusieurs solutions), liste des hypothèses (quand aucune méthode ne fonctionne), liste des archives.
La liste des grilles d’une archive n’apparaît quant à elle que quand on clique sur une archive, dans la liste des archives.
L ’écran de calcul qui apparaît quand on clique sur l’icône de transfert est décrit dans l’Aide, dans un écran séparé, appelé par l’icône
Les 3 types de grilles (implantées dans le programme, créées à partir de revues, générées)
Grilles, au nombre de 151, implantées en dur dans le programme,
Elles se trouvent dans 4 archives de base, non modifiables, non effaçables. Ces 4 archives sont les suivantes :
19 grilles de la littérature de sudoku
73 gilles difficiles générées
50 grilles faciles générées
9 grilles AIC
Les archives 1 et 4 ont été copiées dans des revues ou sur des sites internet. Les archives 2 et 3 ont été générées avec le programme de génération de grille intégré dans ce site de sudoku, et sont donc originales. Une des grilles générées, appelée « pivoine », est volontairement fausse.
Lorsque l’utilisateur sauvegarde une grille, quelle que soit son origine, une archive est créée avec le nom que lui a donné l’utilisateur, au-dessus de la grille, et la grille a le nom que lui a donné l’utilisateur. Si le nom de l’archive est une des 4 archives de base, une archive est créée avec comme nom « Nouvelle archive », et vient se placer après les 4 archives de base, dans la liste des archives. Sauf si cette archive existe déjà, auquel cas la nouvelle grille va se placer à la fin de cette archive.
L’utilisateur peut créer autant d’archives personnelles qu’il le veut, et les grilles personnelles dans ces archives peuvent être en nombre indéfini.
Grilles créées, à partir de grilles trouvées dans des revues ou sur internet
Si l’utilisateur clique sur l’icône de création de grille une grille vierge apparaît, avec le nom de grille N. Le nom de l’archive est inchangé, et est donc le dernier utilisé. L’utilisateur peut modifier ces 2 noms.
Il existe, dans le programme, un clavier virtuel, que l’utilisateur peut afficher s’il sélectionne cette option, dans le tableau des options (qui se trouve dans l’espace de calcul ; il faut consulter l’Aide pour connaître la procédure). Ce clavier virtuel est plus riche que le clavier usuel, avec des chiffres romains, des lettres grecques, des émojis, des caractères de musique, etc. Juste pour le fun.
La procédure pour implanter des chiffres dans les cases vierges est l’une des 2 suivantes :
Avec une souris (comme pour un ordinateur) :
Survoler la grille, jusqu’à la case que vous voulez affecter. Un tableau interne de cette case apparaît avec les chiffres-candidats de cette case (ceux qui sont disponibles, où la case en question ne voit pas une case avec ce chiffre, ni sur la même ligne, ni sur la même colonne, ni sur le même bloc). Si la grille est vierge, tous les chiffres de 1 à 9 apparaissent dans ce tableau interne, pour toutes les cases de la grille.
Pour la grille Amandier ci-dessus, le fait de survoler la case E1 donne le résultat suivant :
Si on clique sur un des chiffres de ce tableau interne, il est affecté à cette case, comme par exemple ici le chiffre 5 , affecté à la case E1:
Avec un écran tactile (comme pour un téléphone portable)
Dans ce cas, il faut appuyer sur la case E1, pour faire apparaître le tableau interne des chiffres-candidats de cette case E1, puis appuyer sur le chiffre 5 de cette case, pour qu’il lui soit affecté.
D ans le cas d’une création de grille, suivre cette procédure jusqu’à ce que la grille soit remplie correctement. Il faut ensuite sauvegarder cette nouvelle grille, en cliquant sur l’icône de sauvegarde
en haut de l’écran, sans oublier de renseigner les noms de la grille et de l’archive qui la contient. Si cette archive n’existe pas encore, elle est créée, avec cette grille comme seul contenu.
G rilles,générées en cliquant sur l’icône de génération de grille, dans l’espace de calcul
Cette génération de grille est pilotée par des critères de génération, à trouver dans l’écran des filtres et options, consultable et modifiable dans l’espace de calcul automatique.
Ces grilles sont générées en disposant des chiffres au hasard, et en vérifiant que, au fur et à mesure, on ne rencontre pas des impossibilités. Si, au bout du nombre prévu de chiffres disposé, la grille est fausse, il faut recommencer, jusqu’à obtention d’un résultat. La procédure est donc longue.
La grille obtenue, si elle est avérée correcte, est d’un niveau de difficulté non prévisible à priori. Celui-ci est le résultat d’un hasard. 7 grilles générées sur 10 sont faciles.
Les 3 types de résolution (manuelle, calcul avec des méthodes, calcul complet)
Résolution manuelle, avec la même procédure que pour la création de grilles (première résolution dite manuelle)
L’affectation de chiffre à une case est donc celle indiquée.
Mais il existe une autre procédure qui vise, non pas à affecter un chiffre à une case, mais, au contraire, à l’éliminer des chiffres-candidats de cette case.
Pour cela, il faut au préalable cliquer sur l’icône de basculement (ou appuyer dessus avec un écran tactile), ce qui fait apparaître l’écran suivant , (exemple avec une autre grille appelée « Bambou ») :
En survolant la case E1, le tableau interne de cette case apparaît :
En cliquant maintenant sur le chiffre 5 de cette case E1, le résultat fait apparaître que la case E1 ne contient plus le chiffre 5 parmi ses chiffres candidats :
Résolution par ordinateur, utilisant 32 méthodes permettant d’éviter les impossibilités et 19 méthodes permettant d’éviter les défauts d’unicité (Deuxième résolution avec calcul par application successive de méthodes)
L a liste des méthodes est appelée en cliquant sur l’icône
Sélectionner une méthode de résolution particulière dans cette liste des méthodes pour vérifier si elle est applicable, auquel cas la liste des variantes de cette méthode est affichée, et tous les chiffres impactés par cette méthode apparaissent en rouge sur le diagramme. Pour la méthode « Sue de coq », le résultat est le suivant :
Les 5 premières variantes de cette méthode (sur 10) sont les suivantes :
Si l’utilisateur clique sur une de ces variantes, elle est sélectionnée, ce qui fait apparaître son résultat, où les chiffres en rouge sur le diagramme sont éliminés. Sous la grille, dans la liste des messages, apparaît l’explication particulière de la méthode utilisée, suivie de l’explication générale de cette méthode :
La première ligne de la liste des méthodes, intitulée « Toutes les méthodes applicables », permet de balayer l’ensemble des méthodes, et de visualiser celles qui sont applicables, les chiffres en rouge sur le diagramme étant ceux qui sont éliminés si on applique toutes ces méthodes. Sous la grille est répertoriée la liste de ces méthodes applicables, avec leurs nombres de variantes. Sous ce message apparaît la liste de toutes les variantes de toutes les méthodes applicables. Pour la grille Bouleau, il y a 82 variantes, au total, dont les 20 premières sont présentées :
I l est possible alors de calculer et afficher la grille obtenue en supprimant les chiffres rouges et en supprimant aussi les chiffres des cases voyant le chiffre dans une case affectée, en cliquant sur l’icône en haut de la liste des variantes
On peut même recommencer la procédure, sur cette nouvelle grille, de sélectionner toutes les méthodes applicables, puis de supprimer les chiffres rouges :
I l apparaît cette fois 41 variantes, dans la liste des variantes de toutes les méthodes applicables, dont les 3 premières sont affichées. Il est possible de sélectionner l’une de ces 41 variantes pour en voir l’effet : chiffres en rouge de la grille, et explication particulière et générale de la méthode utilisée dans la zone des messages. Il est de nouveau possible ensuite de calculer et afficher la grille obtenue, en supprimant les chiffres rouges et en supprimant aussi les chiffres des cases voyant ce chiffre dans une case affectée, en cliquant sur l’icône en haut de la liste des variantes
Il est même possible de recommencer encore cette procédure, ce qui va permettre d’afficher la solution ! Pour des grilles faciles, il faut entre 2 et 4 itérations pour trouver la solution. Cette manière de faire ne fonctionne pas avec des grilles où il est nécessaire de faire des hypothèses, car aucune méthode, parmi les 32 existantes, n’est applicable.
L’un des avantages de cette résolution de grilles, par l’utilisation intensive des méthodes de résolution, est de balayer ces méthodes et donc d’identifier d’éventuels bugs. 4 de ces bugs ont été ainsi résolus en un mois (La griffe du tigre, 3D Medusa, Jellyfish, Squirmbag) , et il en reste 2, en cours de traitement (AIC Chain, Quadruples).
Très important : L’identification d’un bug peut se faire par l’apparition de chiffres en rouge à éliminer, alors qu’ils font partie de la solution.
Lancer un calcul par ordinateur en cliquant sur l’icône dans l’espace automatique (troisième résolution de grilles, seule à même de résoudre des grilles avec hypothèse)
Cela permet de calculer, étape par étape, la résolution de la grille, avec affichage du résultat final (le programme sait calculer toutes les grilles, sans exception, en en vérifiant la validité).
La grille « Bouleau » dans l’espace de calcul, obtenue après avoir cliqué sur l’icône
dans son espace manuel :
L e calcul de cette grille peut s’effectuer de 2 manières, selon l’icône sur laquelle on clique (ou on appuie) :
pour un calcul complet utilisant l’ensemble des 32 méthodes
pour un calcul réduit n’utilisant que les méthodes les plus simples, dont le nombre est défini dans l’écran des filtres et options
Voici la grille solution obtenue en lançant un calcul utilisant toutes les 32 méthodes :
La liste des 46 étapes de calcul pour y parvenir est la suivante :
Pour des grilles plus difficiles, il faut passer par des hypothèses, parfois en cascade, dont le nombre peut être important, même avec toutes les 32 méthodes de résolution.
Voici l’exemple de la grille, d’origine finlandaise, dénommée « Al Escargot ». Elle se trouve en dur, dans le programme, dans l’archive de base « 19 grilles de la littérature de sudoku ».
Quand on lance le calcul complet de cette grille, cela nécessite 10 hypothèses. La durée de calcul est de 2 minutes sur ordinateur, et de 30 minutes sur téléphone portable :
La solution est trouvée lors de l’hypothèse 5, en 36 étapes de calcul, toutes les autres hypothèses aboutissant à une impossibilité.
Le développement d’applications
Historique succincte de la programmation informatique
La programmation sur ordinateur a commencé dans la années 1960, sur d’énormes machines des entreprises Control Data et IBM.
Les premiers langages étaient le langage machine et l’assembleur. Très vite de nouveaux langages sont apparus : Basic, Fortran (applications scientifiques), Pascal, C et C++. Mais aussi Cobol (comptabilité), LISP, SQL (gestion de tableaux).
Avec l’avènement des premiers microprocesseurs, au début des années 1980, ce fut Java.
L’avènement d’internet
C’est l’avènement d’internet au début des années 2000 qui marqua la véritable essor de l’informatique, avec le développement des ordinateurs en réseau, dont la puissance a dépassé les gros systèmes.
Le mode natif internet (HTML, CSS, javascipt) a fait l’objet du développement W3C (World Wide Web), avec des millions de développeurs dans le monde.
De nouveaux langages sont apparus : PHP et Mysql, Java, Swift, Python (pour l’Intelligence Artificielle).
De nouvelles couches logicielles se sont ajoutées au mode natif internet, appelées frameworks, permettant de gérer la majorité des applications du Web (Banques, Assurances, process industriels, comptabilité): React JS, Angular, Flask, KOA pour Node JS, Django, Express, Ruby on rails, Spring, Bootstrap.
Une nouvelle manière de développer des applications sur internet
La communauté des développeurs s’est renforcé de groupes communautaires comme Github.
Et surtout l’aide en ligne est devenu un outil indispensable pour la programmation en mode natif internet. Le meilleur site, fonctionnant de manière efficace avec des exemples est W3Schools. C’est ce dont a bénéficié le développement de l’application de sudoku sur internet, sur le site www.sudokunew.com, dont le code est disponible en open source.
Le savoir-faire acquis en 10 ans pour le développement de l’application de sudoku sur internet, peut être décliné pour d’autres applications, essentiellement dans le domaine des jeux, comme le bridge. C’est ce que propose de faire le développeur de ce site de sudoku.
Le cahier des charges d’un logiciel de bridge
Les données
Les données de départ sont les suivantes :
La vulnérabilté : Personne, NS, EO, Tous
Le donneur : Ouest, Nord, Est, Sud
La main de l’utilisateur (13 cartes)
Au fur et à mesure du déroulement des enchères : le tableau des enchères et le contrat final
La carte d’entame
La main du mort : 13 cartes
Au fur et à mesure du déroulement du jeu de la carte : le tableau des cartes jouées
L’interface d’accueil
Elle contient :
Les données de départ
Le tableau des enchères possibles
Les enchères successives jusqu’au contrat final
Les cartes jouées au fur et à mesure
Cela sera présent dans l’interface d’accueil.
Les enchères
Ces enchères obéissent à certaines règles :
Toute enchère produite autre que passe, contre et surcontre, doit être supérieure à la dernière enchère
Chaque joueur joue à son tour
Les enchères produites doivent être conformes à ce qui est écrit dans la feuille de convention du joueur, et son partenaire doit fournir la bonne explication à la demande de son adversaire à qui c’est le tour de parler
La feuille de convention
La feuille de convention des enchères proposée est celle du standard français. Les enchères doivent consister en un dialogue entre partenaires, et, à contrario, en un conflit avec les adversaires.
Le principe du dialogue à 2 est de trouver le meilleur contrat, en faisant en sorte, au fur et à mesure que les enchères progressent, d’approcher ce contrat final, sans dépasser la ligne rouge qui consisterait à aller au-delà du contrat optimum. C’est le joueur qui possède le plus d’éléments de la décision finale, qui choisit le contrat final, souvent celui qui s’est le moins décrit. Il est parfois nécessaire d’enchérir progressivement, les jumps intempestifs étant réservés à des mains non distribués difficiles à décrire. Le risque est souvent le passe intempestif du partenaire qui doit avoir comme principe de ne pas passer s’il a le moindre doute..
Autre principe important : continuer les enchères tant qu’on n’a pas donné le plein de sa main. Les enchères paresseuses sont à bannir : ne pas conclure tant qu’il existe une chance d’améliorer le contrat. Le bon arbitrage pour prendre la bonne décision est celui où le joueur a tous les éléments de cette décision, ni plus ni moins.
Et privilégier le fit à la description d’une nouvelle couleur, ce qui permet de prendre la bonne décision. Réciproquement, intervenir pour gêner les adversaires ou les pousser à la faute. Comme le disait un champion de mes amis : « Je l’ai mis au bord de la piscine, et il a plongé ! ».
Les ouvertures et les réponses du standard français
Majeure 5ème, meilleure mineure
1SA 15-17 H avec Stayman et Texas
2♣ fort indéterminé, avec relais à 2♦ pour ensuite annoncer une couleur d’au moins 20 DH ou 2SA 22-23 H
2♦ Forcing de manche, interrogative aux as avec réponse codifiée
2♥ : pas d’as sans jeu
2♠ : un as majeur
2SA : pas d’as avec du jeu ou 2 rois
3♣ : l’as de ♣
3♦ : l’as de ♦
3SA : 2 as
3♥ ou 3♠ : couleur 5ème ou plus avec RD sans rien à côté
4SA : 3 as
2♥ ou 2♠ : Faible 6-9 H avec 6 cartes
2SA : 20-21 H sans courte
3 dans une couleur ou plus : barrage
3SA : Mineure affranchie sans rien à côté. Le partenaire peut passer s’il tient les autres couleurs.
Les interventions derrière l’ouverture
L’intervention à la couleur :
Au niveau le plus bas : intervention naturelle, avec au moins 8H+.
Avec un niveau plus élevé : tendance barrage
Le contre d’appel :
Enchère fourre-tout avec du jeu
L’intervention 1SA :
15-17 H sans courte et contrôle de l’ouverture
Les bicolores (Michaël non précisé) :
2SA pour les moins chères, sinon annonce naturelle de la plus chère.
Le cue bid :
Main forte, impliquant le fit si le partenaire a déjà parlé.
Les jumps :
Barrage avec une main faible ou, au contraire, main forte forcing dans un dialogue à deux.
Le 4SA quantitatif :
Propositionnel de chelem.
Les enchères compétitives :
Naturelles souvent pour montrer une entame, ou parfois pour pousser les adversaires à la faute.
Les barrages
A la différence des jumps, les barrages ont pour fonction, non pas de se décrire, mais de gêner les adversaires dans leur recherche du meilleur contrat. Ils ont donc une fonction destructrice, comme les psychics, qui donnent une description erronée de sa main.
Le Blackwood 5 clés
Les 5 clés sont les 4 as et le roi d’atout.
Toujours à 4SA avec réponses :
5♣ = 30 (3 clés ou 0 clé)
5♦ = 41 (4 clés ou 1 clé)
5♥ = 2 (2 clés)
5♠ = 2 (2 clés et la dame d’atout).
Le jeu de la carte
Le déclarant
Le plan de jeu du déclarant consiste à identifier les gagnantes directes, les perdantes directes, les gagnantes potentielles et les perdantes potentielles.
Le jeu de la carte en découle. Il faut se concentrer sur les gagnantes potentielles et les perdantes potentielles.
Les gagnantes potentielles sont celles du triptyque impasse-coupe-affranchissement, en y ajoutant le squeeze.
Les perdantes potentielles sont similaires aux gagnantes potentielles. Il existe une course de vitesse entre le déclarant et la défense, pour valoriser l’une ou l’autre. Dans cette course de vitesse, il y a un ordre de priorité, en particulier n’effectuer les impasses qu’en dernier, parce que c’est du tout ou rien, sauf si elles sont absolument nécessaires à la réussite du contrat.
Ce qui guide le plan de jeu, concerne les statistiques sur les distributions, les nécessités absolues, les nécessités relatives.
Certaines gagnantes n’apparaissent qu’en dernier ressort, comme les squeezes et les impasses.
Parmi les indices orientant le jeu de la carte, il faut tenir compte de ce qu’ont révélé les enchères (en cas d’intervention adverse), des cartes déjà tombées, de ce qu’ont révélé les défausses (appels, pair-impair). Le flanc a parfois intérêt à fausser la parité pour tromper le déclarant.
La course à l’affranchissement fait partie des objectifs du déclarant et de la défense.
Le contrôle du coup est essentiel, pour ne pas être débordé, comme de laisser traîner un atout, ou de donner un coup à blanc, ou encore d’éviter la main dangereuse (celle qui a des levées à prendre) en orientant les impasses ou les remises en main de l’autre côté.
Le squeeze consiste à forcer la défense, qui contrôle 2 ou 3 couleurs, à devoir défausser, en fin de coup, un de ces contrôles.
La prise de risque est nécessaire, en se basant sur ce que feront les autres déclarants, ce que l’on appelle le champ. Pour bien réussir au bridge, il vaut mieux se référer à ce champ, pour se comparer à eux. Le tout ou rien est à bannir. La sagacité d’un bon déclarant se juge à la manière de gérer les situations compliquées, à évaluer le rapport bénéfices/risques d’une prise de risque. Il vaut souvent mieux gagner avec un petit bénéfice, mais sans risque, que de chercher l’aventure avec des risques inconsidérés. Mais une bonne évaluation du risque calculé est source de gros bénéfices, et n’est donc pas à négliger.
Une situation particulière est celle où le déclarant est embarqué dans un contrat aberrant, où il doit donc prendre tous les risques ; car, un zéro étant un zéro, il n’y a quasiment rien à perdre à chercher les risques supplémentaires.
A contrario, quand le contrat est bon, il vaut mieux assurer que de chercher à améliorer. Le mieux est l’ennemi du bien.
La défense
La défense est un domaine difficile, car il s’agit de bien s’entendre avec son partenaire, pour savoir où communiquer, comment compliquer la tâche du déclarant, et à contrario de ne pas lui faciliter la tâche.
Bien montrer la parité, pour que le partenaire connaisse la distribution : défausser en montant montre un nombre impair de cartes dans la couleur.
L’entame est un domaine compliqué, car cela démarre le jeu de la carte, et le joueur n’a comme indices que les enchères. C’est là où des enchères pas trop explicites complique la tâche de l’entameur.
Le plan de jeu de la défense consiste à compliquer la tâche du déclarant en lui posant des problèmes. Il faut toujours viser à créer des incertitudes chez le déclarant.
Bien s’entendre avec son partenaire est essentiel sur la signification des défausses : appel direct ou pas, parité, levinthal, appel préférentiel.
Conclusion
Le logiciel de sudoku réalisé sur le site internet www.sudokunew.com est une réussite, montrant ce qu’il est possible de faire en n’utilisant que les langages de base internet, en s’appuyant sur les progrès réalisés sur ces langages par les millions de développeurs dans le monde, et aussi sur les sites d’aide comme W3Schools.
Ce savoir-faire acquis en s’appuyant sur la réalisation de ce site de sudoku peut être décliné pour d’autres applications, essentiellement dans le domaine du jeu. C’est ce que propose de faire Raoul SALZBERG, l’auteur de ce site de sudoku, en réalisant un site de bridge dans les 6 mois qui viennent.
Ce site de bridge démontrera la validité du concept de développement d’applications sur internet, uniquement avec les langages du mode natif internet.
Naturellement, pour bénéficier de ce savoir-faire, il est nécessaire d’en comprendre le mécanisme. Ce qui, mécaniquement, nécessite une activité de formation et de conseil.







































留言